【統計】中心極限定理をR言語で実験してみた
最近、統計の勉強をしている。ちょっと前に流行ったこの本(の続編?)を読んでいるのだが、その中の「中心極限定理」の説明が分かりやすかったので、R言語で実験してみた。
![統計学が最強の学問である[実践編]---データ分析のための思想と方法 統計学が最強の学問である[実践編]---データ分析のための思想と方法](http://ecx.images-amazon.com/images/I/51XOoTJwsiL._SL160_.jpg)
統計学が最強の学問である[実践編]---データ分析のための思想と方法
- 作者: 西内啓
- 出版社/メーカー: ダイヤモンド社
- 発売日: 2014/10/24
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (5件) を見る
中心極限定理とは、「どんな分布(たとえ正規分布でなくても!)のデータでもいくつかの数をサンプリングして平均する、という操作を十分な回数繰り返すと、その平均値の分布は正規分布となる」という意味だと理解している。直感的にはよく分かりづらいが、簡単に実験できそうだったのでR言語で試してみた。
サイコロの目の平均値
サイコロの目は1から6まで全ての値が出る確率は等しい1/6だと言える。このサイコロを100回振って目の平均値を求める、という操作を10,000回とか十分大きな回数だけ行うとする。そうした場合、その平均値の分布は正規分布に従う、というもの。
そこで、Rで以下のようなコードでこの実験を行ってみる。
# サイコロを100回振ったときの目の平均を求める実験を10000回繰り返す par(mfrow=c(1,2)) ## 元のデータの分布 sai.data <- sample(6,100, replace=TRUE) hist(sai.data) ## 平均の分布 sai.means <- sapply(c(1:10000), function(x) {mean(floor(runif(100, 1, 7)))} ) hist(sai.means)
これによって、以下のヒストグラムが得られる。
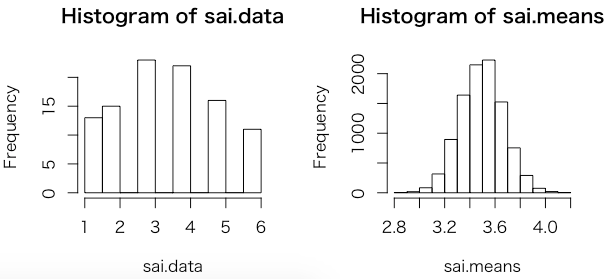
左の図のsai.dataはサイコロを100回振ったときのヒストグラムを表す。1/6のランダムだが、多少の隔たりは毎回起こりうる。これは当然正規分布ではない。
一方、右の図のsai.meansは100回サイコロを振った平均値を10,000回求め、それぞれの平均値のヒストグラムを書くと、確かに約3.5を中心とした正規分布になっている!
ちなみに3.5という値は1回のサイコロを振ったときの目の期待値に一致している。

歪んだコインの表・裏の回数の平均値
続いて、割合が一様でない例で考えるために、歪んだコインを投げて表・裏が出る回数について考えてみる。このコインは表が出る確率が1/3, 裏が出る確率が2/3とする。
このコインを100回投げて表が出る回数と裏が出る回数をそれぞれカウントする、という操作を10,000回繰り返し、やはり表が出る回数の平均と、裏が出る回数の平均をそれぞれヒストグラムで描画してみる。
Rの実装は以下の通り。
# 表が2/3、裏が1/3の確率で出るコインを100回投げたときの # 表、裏それぞれの出た回数の平均を求める実験を10000回繰り返す par(mfrow=c(1,2)) # n回コインを投げ、その結果の表を返す flip_coin <- function(n) { table(sample(c("表","裏"), n, prob=c(2:1), replace=TRUE)) } # データの分布 coin.data <- flip_coin(100) coin.data # 平均の分布 coin.dataset <- sapply(c(1:10000), function(x) {flip_coin(100)} ) coin.means.omote <- coin.dataset["表",] coin.means.ura <- coin.dataset["裏",] hist(coin.means.omote) hist(coin.means.ura)
このコードを実行する。途中、データ分布を1度だけ表示しているが、これは以下のような結果となる。
> coin.data 表 裏 65 35
このことから、確かに表と裏がだいたい2:1の割合となっていることが分かる。
さらにヒストグラムは以下のようになる。

左のヒストグラムが表の出た回数、右のヒストグラムが裏の出た回数となる。
これは中心の位置が割合に応じてずれているものの、形状自体はほぼ正規分布と言える!
まとめ
中心極限定理は、元データの分布に関わらず、そこからサンプリングしたデータを平均するという操作を十分に繰り返すと正規分布が得られるというものだが、今回はそれをサイコロ、コインという身近な例で確かめた。
統計は身近なデータで実験ができるが、数学的に抽象的な説明ばかりだといまいち納得感が得られないこともあるが、Rでさくっと手元で動かしてみるとその意味がよく理解できた。
※統計は今このあたりの本で勉強してます。

- 作者: 西内啓
- 出版社/メーカー: ダイヤモンド社
- 発売日: 2013/01/24
- メディア: 単行本(ソフトカバー)
- 購入: 11人 クリック: 209回
- この商品を含むブログ (127件) を見る
![統計学が最強の学問である[実践編]---データ分析のための思想と方法 統計学が最強の学問である[実践編]---データ分析のための思想と方法](http://ecx.images-amazon.com/images/I/51XOoTJwsiL._SL160_.jpg)
統計学が最強の学問である[実践編]---データ分析のための思想と方法
- 作者: 西内啓
- 出版社/メーカー: ダイヤモンド社
- 発売日: 2014/10/24
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (5件) を見る

- 作者: 山田剛史,杉澤武俊,村井潤一郎
- 出版社/メーカー: オーム社
- 発売日: 2008/01/25
- メディア: 単行本
- 購入: 64人 クリック: 782回
- この商品を含むブログ (68件) を見る